Olá, pessoal! Neste post, vamos resolver juntos a questão 5 do Exame Discursivo de matemática do vestibular da UERJ 2025. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Os quadrados 
, 
e 
têm os lados 
, 
e 
contidos na base 
do triângulo 
, ilustrado a seguir. Os pontos 
e 
pertencem ao lado 
, e os pontos 
e 
ao lado 
, do mesmo triângulo.
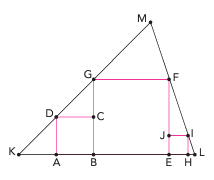
São conhecidas as seguintes medidas: 
cm, 
cm e 
cm. Calcule, em cm
, a área do triângulo 
.
Resposta
24 cm
Resolução
Em primeiro lugar, vamos observar a figura abaixo:
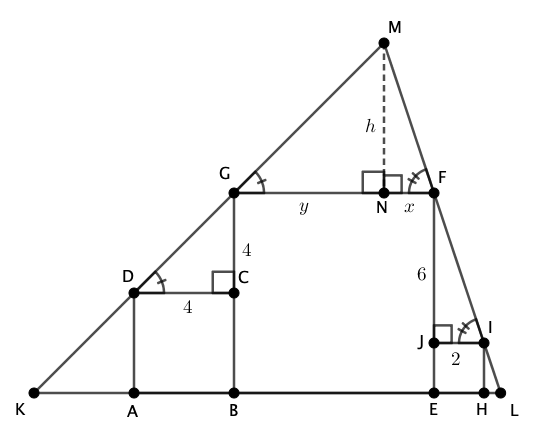
Temos que:
. Logo, 
e, consequentemente:![\[\begin{array}{rl}& \dfrac{4}{y} = \dfrac{4}{h} \Leftrightarrow \\ \Leftrightarrow & y = h; \end{array}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDgiIGhlaWdodD0iNTkiIHZpZXdCb3g9IjAgMCAxMDggNTkiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+ "Rendered by QuickLaTeX.com")
. Logo, 
e, consequentemente:![\[\begin{array}{rl} & \dfrac{2}{x} = \dfrac{6}{h} \Leftrightarrow \\ \Leftrightarrow & x = \dfrac{h}{3}. \end{array}\]](data:image/svg+xml;base64,PHN2ZyB4bWxucz0iaHR0cDovL3d3dy53My5vcmcvMjAwMC9zdmciIHdpZHRoPSIxMDgiIGhlaWdodD0iNzIiIHZpZXdCb3g9IjAgMCAxMDggNzIiPjxyZWN0IHdpZHRoPSIxMDAlIiBoZWlnaHQ9IjEwMCUiIHN0eWxlPSJmaWxsOiNjZmQ0ZGI7ZmlsbC1vcGFjaXR5OiAwLjE7Ii8+PC9zdmc+ "Rendered by QuickLaTeX.com")
. Logo, 
e, consequentemente:![\[\begin{array}{rl}& \dfrac{4}{y} = \dfrac{4}{h} \Leftrightarrow \\ \Leftrightarrow & y = h; \end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-5a06c89999421c9744b83c1cc56a8926_l3.png "Rendered by QuickLaTeX.com")
. Logo, 
e, consequentemente:![\[\begin{array}{rl} & \dfrac{2}{x} = \dfrac{6}{h} \Leftrightarrow \\ \Leftrightarrow & x = \dfrac{h}{3}. \end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-aceb30046b1b17b072bc6ac36dd97f3c_l3.png "Rendered by QuickLaTeX.com")
Além disso,
![\[\begin{array}{rl}& x+y = 8 \Leftrightarrow \\\Leftrightarrow & h + \dfrac{h}{3} = 8 \Leftrightarrow\\\Leftrightarrow & 3h + h = 8 \cdot 3 \Leftrightarrow\\\Leftrightarrow & 4h = 24 \Leftrightarrow\\\Leftrightarrow & h = \dfrac{24}{4} \Leftrightarrow\\\Leftrightarrow & h = 6\text{ cm}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-c1c9a09a6f998470848832f1dd4394b1_l3.png "Rendered by QuickLaTeX.com")
Portanto, a área do triângulo
é igual a: ![\[\begin{array}{rl}& \dfrac{GF \times h}{2} \\= & \dfrac{8 \times 6}{2}\\= & \dfrac{48}{2}\\= & 24 \text{ cm}^2.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-1bd4b0c3b8e6749492ecf18d002124c3_l3.png "Rendered by QuickLaTeX.com")
