Olá, pessoal! Neste post, vamos resolver juntos a questão 8 do Exame Discursivo de matemática do vestibular da UERJ 2025. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Uma doceira, que vende trufas de cerejas e de nozes, tem a encomenda fixa semanal de 200 trufas de cerejas (C) e de 150 de nozes (N). Se houver demanda, ela consegue fazer, no máximo, 600 trufas por semana. Os lucros por unidade vendida de C e N são, respectivamente, R$ 4,00 e R$ 3,00.
Considerando que a doceira faça, por semana, ![]() unidades de C e
unidades de C e ![]() de N, valem as seguintes desigualdades:
de N, valem as seguintes desigualdades:
![Rendered by QuickLaTeX.com \[\left\{\begin{array}{l}x \geq 200\\y \geq 150\\x+y \leq 600\end{array}\right.\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-4b4b4e7097147de7c5e8b1df7091e026_l3.png)
Os pares
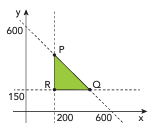
Calcule, em reais, o lucro de apenas uma encomenda fixa semanal. Calcule, em reais, também, o lucro semanal máximo que a doceira pode obter com a venda de 600 trufas.
Resposta
Lucro da encomenda fixa: R$ 1.250,00
Lucro máximo: R$ 2.400,00
Resolução
Na encomenda fixa semanal, são vendidas 200 trufas de cereja e 150 trufas de nozes. Logo, o lucro para esta encomenda é igual a:
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& \text{R\$ } 4,00 \cdot 200 + \text{R\$ } 3,00 \cdot 150 \\= & \text{R\$ } 800,00 + \text{R\$ } 450,00\\= & \text{R\$ } 1.250,00.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-e26e13b86d3b38cedc8c84095cfef882_l3.png)
Agora, vamos calcular o lucro semanal máximo com a venda de 600 trufas. Temos que o lucro
![]()
![]()
![Rendered by QuickLaTeX.com \[\begin{array}{rcl} L & \leq & \text{R\$ } 4,00 \cdot x + \text{R\$ } 3,00 \cdot \left(600 - x\right)\\ & \leq & \text{R\$ } 4,00 \cdot x + \text{R\$ } 1.800,00 - \text{R\$ } 3,00 \cdot x\\ & \leq & \text{R\$ } 1,00 \cdot x + \text{R\$ } 1.800,00.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-c1c4cfe0ceae5495d6c17d3e2a738da5_l3.png)
Portanto, o lucro máximo é igual a
![Rendered by QuickLaTeX.com \[\begin{array}{rl} & \text{R\$ } 1,00 \cdot 600 + \text{R\$ } 1.800,00 \\ = & \text{R\$ } 600,00 + \text{R\$ } 1.800,00 \\ = & \text{R\$ } 2.400,00.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-c7694ee2c442f80f40712d0d7fbd83d6_l3.png)


