Olá, pessoal! Neste post, vamos resolver juntos a questão 10 da prova objetiva de matemática do vestibular da FGV 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
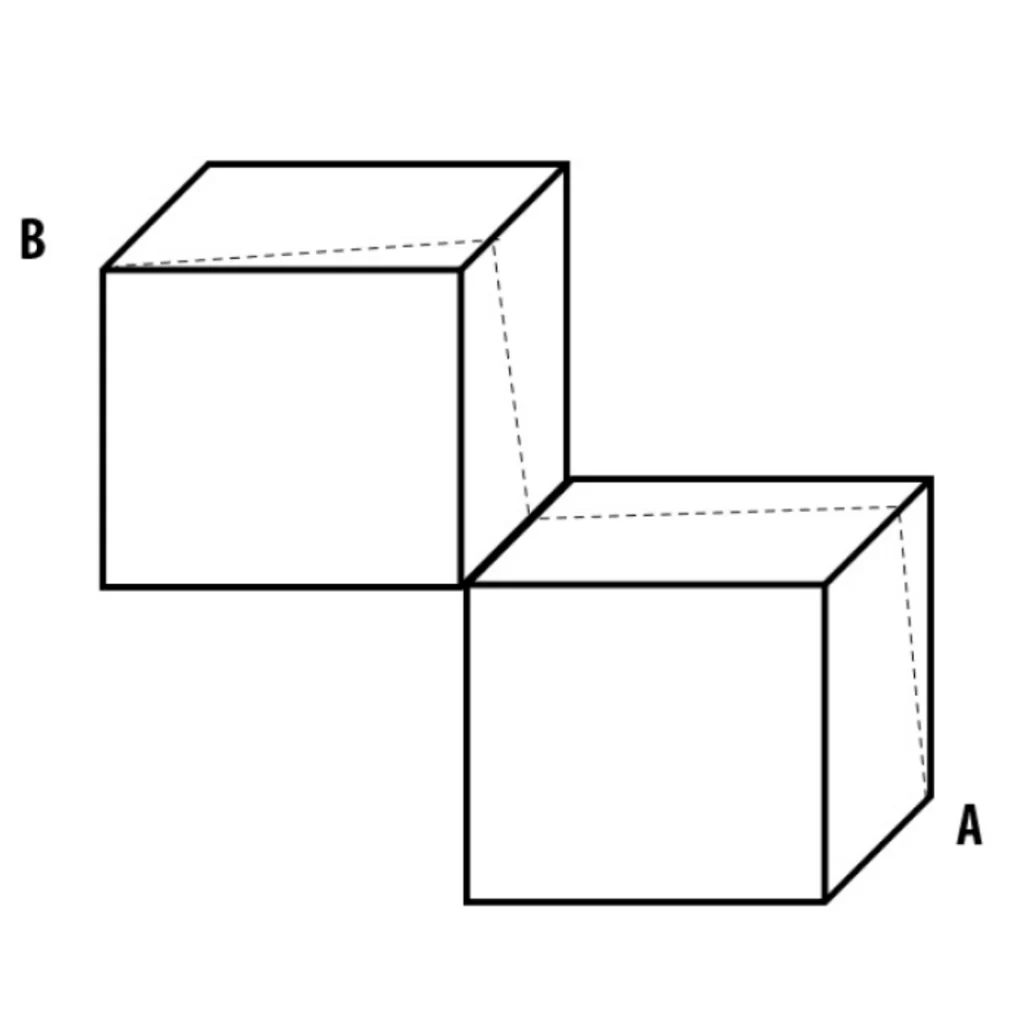
A figura abaixo exibe um sólido formado por dois cubos idênticos, que compartilham uma aresta (como se fossem dois degraus de uma escada). As faces dos cubos que compartilham a aresta citada são perpendiculares. Estão destacados na figura os vértices A e B, cada um em um cubo. Sobre a superfície dos cubos, foi traçada a linha de menor comprimento que liga o vértice A ao vértice B. Sabendo-se que os cubos têm aresta igual a 1, o comprimento da linha traçada é
(A) 
(B) 
(C) 
(D) 
(E) 
Gabarito: B
Resolução:
A menor distância entre dois pontos é a medida do segmento de reta que os une. Para que a gente possa calcular o menor caminho que leva de 
até 
, precisamos calcular a medida do segmento de reta 
na planificação das faces dos cubos por onde esse caminho passa.
Observe a figura abaixo:
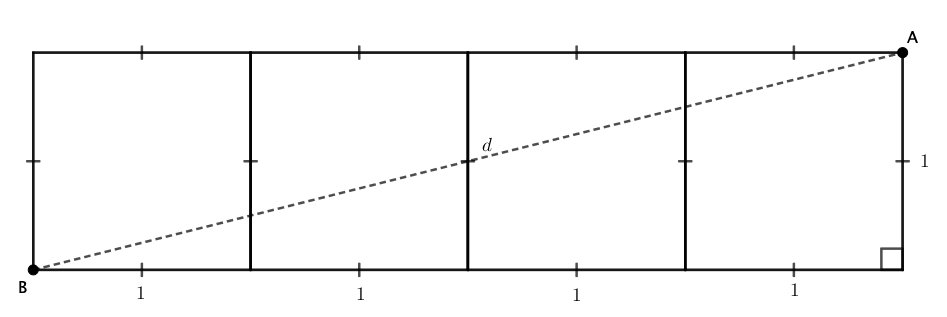
Aplicando o Teorema de Pitágoras, temos que:
![\[\begin{array}{rl} & d^2=1^2+4^2 \Leftrightarrow\\\Leftrightarrow & d^2 = 1 + 16 \Leftrightarrow\\\Leftrightarrow & d^2 = 17 \Rightarrow\\\Rightarrow & d=\sqrt{17}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-bfab55de5a7968696b4ba7d0fa6964e4_l3.png "Rendered by QuickLaTeX.com")
Portanto, o gabarito é a letra B.
