Olá, pessoal! Neste post, vamos resolver juntos a questão 11 da prova objetiva de matemática do vestibular da FGV 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Seja 
uma função tal que 
, para quaisquer 
e 
reais maiores do que 0 (zero).
Se 
, então o valor de 
é:
(A) 12
(B) 25
(C) 16
(D) 32
(E) 24
Gabarito: C
Resolução:
A lei de formação da função é dada pela razão entre dois números.
Além disso, temos 
e queremos encontrar o .
Logo, a ideia é encontrar um número que seja simultaneamente múltiplo de 48 e de 60.
Vamos então buscar o m.m.c. de 48 e 60:
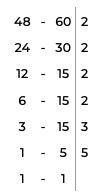
Pelo diagrama acima, temos que m.m.c.(48,60) = 
.
Logo, podemos afirmar que:
![\[\begin{array}{rl} & f(48) = f\left(\dfrac{240}{5}\right) \Leftrightarrow\\[1em]\Leftrightarrow & f(48)=5\cdot f(240) \Leftrightarrow\\\Leftrightarrow & 5 \cdot f(240) = 20 \Lefrightarrow\\\Leftrightarrow & f(240) = 4.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-4fc0ec2d4ce3c71bba03e95ee273ee06_l3.png "Rendered by QuickLaTeX.com")
Consequentemente, temos que:
![\[\begin{array}{rcl}f(60) & = & f\left(\dfrac{240}{4}\right)\\[1em] & = & 4\cdot f(240)\\ & = & 4 \cdot 4\\ & = & 16.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-cd9e17b8e17c292a657d43f917f33acc_l3.png "Rendered by QuickLaTeX.com")
Portanto, o gabarito é a letra C.
