Olá, pessoal! Neste post, vamos resolver juntos a questão 12 da prova objetiva de matemática do vestibular da FGV 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Uma longa folha de papel retangular foi enrolada em torno de um tubo cilíndrico formando um rolo de papel de formato também cilíndrico. A circunferência externa da base deste rolo tem raio 
cm. O tubo cilíndrico no centro do rolo tem como base uma circunferência de raio 
cm.
Sabendo-se que a folha de papel tem espessura de 0,01 cm e usando-se a aproximação 
, o comprimento, em metros, da folha de papel é, aproximadamente,
(A) 200
(B) 180
(C) 190
(D) 175
(E) 225
Gabarito: E
Resolução:
Observe a figura abaixo:
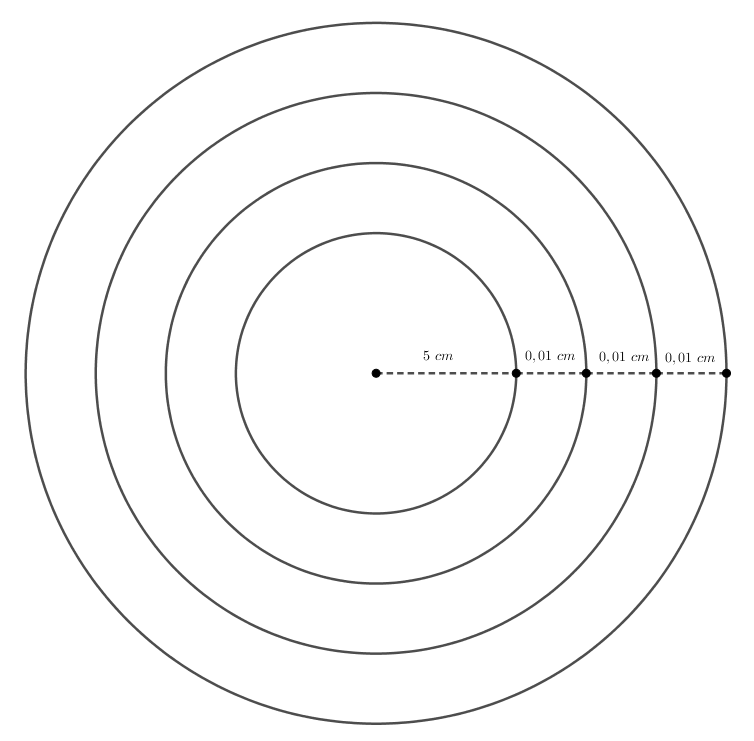
Como estamos enrolando a folha nesse rolo e, além disso, o comprimento de uma circunferência é igual a 
, temos que o comprimento da folha é igual a:
![\[\begin{array}{rl} & 2\pi \cdot 5 + 2\pi \cdot 5,01 + 2\pi \cdot 5,02 + \\& \ldots + 2\pi \cdot 10\\= & 2\pi \cdot \left(5 + 5,01 + 5,02 + \ldots + 10\right)\\= & 2 \cdot 3 \cdot \frac{(5+10)}{2} \cdot n\\= & 45n\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-350ed09ae04653a6b211b4dfaa85c18d_l3.png "Rendered by QuickLaTeX.com")
Repare que não sabemos o número de termos dessa progressão aritmética.
Então, para continuarmos a resolver este problema, devemos encontrar o valor de
.Sendo assim, repare que:
![\[\begin{array}{rl}& 5 + (n-1) \cdot 0,01 = 10 \Leftrightarrow\\\Leftrightarrow & (n-1) \cdot 0,01 = 5 \Leftrightarrow\\\Leftrightarrow & n-1 = 500 \Leftrightarrow\\\Leftrightarrow & n = 501.\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-98e9a20ab39d603364596339a2e7ebb0_l3.png "Rendered by QuickLaTeX.com")
Consequentemente, o comprimento da folha é igual a:
![\[45 \cdot 501 = 22.545 \text{ cm} = 225,45 \text{ m}.\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-d8e2bff111df3c588538d24f3d925453_l3.png "Rendered by QuickLaTeX.com")
Portanto, o gabarito é a letra E.
