Olá, pessoal! Neste post, vamos resolver juntos a questão 15 da prova objetiva de matemática do vestibular da FGV 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
A curva da figura abaixo é chamada de espiral logarítmica. Todos os pontos 
desta curva são tais que 
e 
, para algum valor real 
.
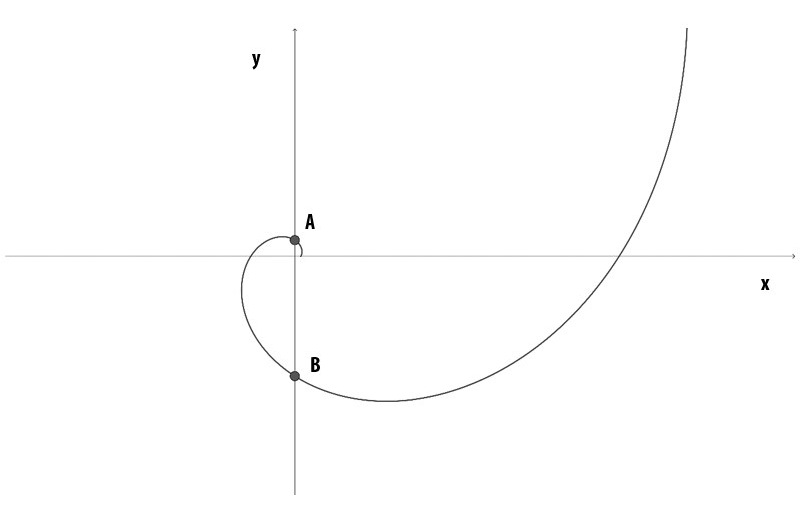
O ponto B é o ponto onde a curva intersecta a parte negativa do eixo Y com o menor valor de 
possível. O valor da ordenada (coordenada Y) do ponto B é
(A) 
(B) 
(C) 
(D) 
(E) 
Gabarito: A
Resolução:
Temos que o ponto 
possui abcissa igual a zero, uma vez que ele se encontra no eixo 
.
Assim, temos que:
![\[\begin{array}{rcl} & \underbrace{2^t}_{>0} \cdot \cos\left(\dfrac{\pi}{2}\cdot t\right) = 0 & \Leftrightarrow\\\Leftrightarrow & \cos\left(\dfrac{\pi}{2}\cdot t\right) = 0\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-004f10d48891d53b438ab63d1fdaba44_l3.png "Rendered by QuickLaTeX.com")
Além disso, a ordenada de
é negativa. Como 
, então devemos ter 
.Mas, uma vez que
, podemos concluir que 
.Logo, temos que:
![\[\begin{array}{rcl} & \dfrac{\pi}{2}\cdot t = \dfrac{3\pi}{2}+2k\pi,\ k \in \mathbb{Z}_{+}& \Leftrightarrow\\\Leftrightarrow & t = 3 + 4k,\ k \in \mathbb{Z}_{+}\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-7bcd4553cbded831f26e067e28ba2833_l3.png "Rendered by QuickLaTeX.com")
Assim,
.Dessa forma, o menor valor possível de
é igual a 3.Consequentemente, a ordenada do ponto
é igual a: ![\[2^3 \cdot \sin \left(\dfrac{3\pi}{2}\right) = 8 \cdot (-1) = -8.\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-b763e1a2abea0eb5679d30f7ec7f5c96_l3.png "Rendered by QuickLaTeX.com")
Portanto, o gabarito é a letra A.
