Olá, pessoal! Neste post, vamos resolver juntos a questão 8 da prova objetiva de matemática do vestibular da FGV 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Em torno de uma mesa circular, há 25 cadeiras igualmente espaçadas e 
pessoas sentadas, de modo que não há pessoas sentadas em cadeiras adjacentes, mas a próxima pessoa a sentar terá que sentar, necessariamente, em uma cadeira adjacente a uma pessoa já sentada. O valor mínimo de é:
(A) 10
(B) 9
(C) 12
(D) 7
(E) 8
Gabarito: B
Resolução:
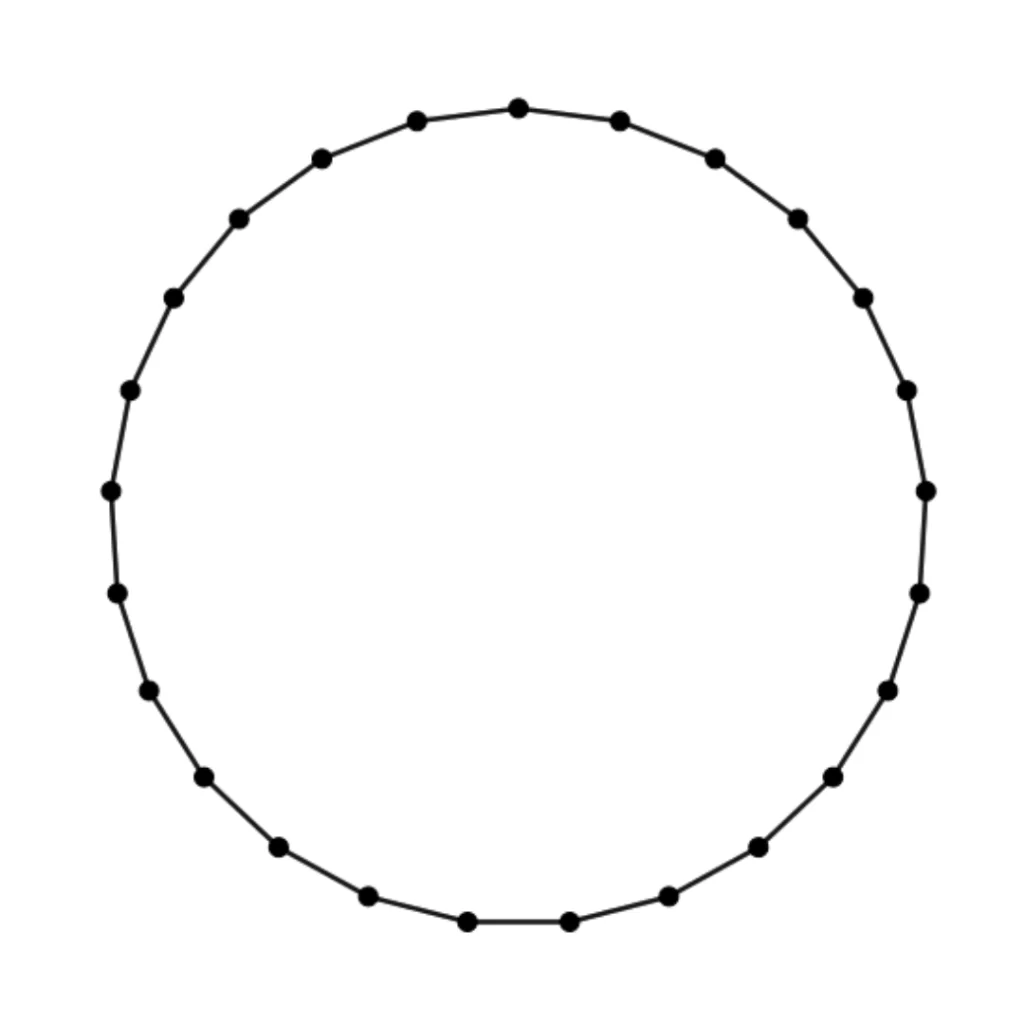
Observe a figura abaixo:
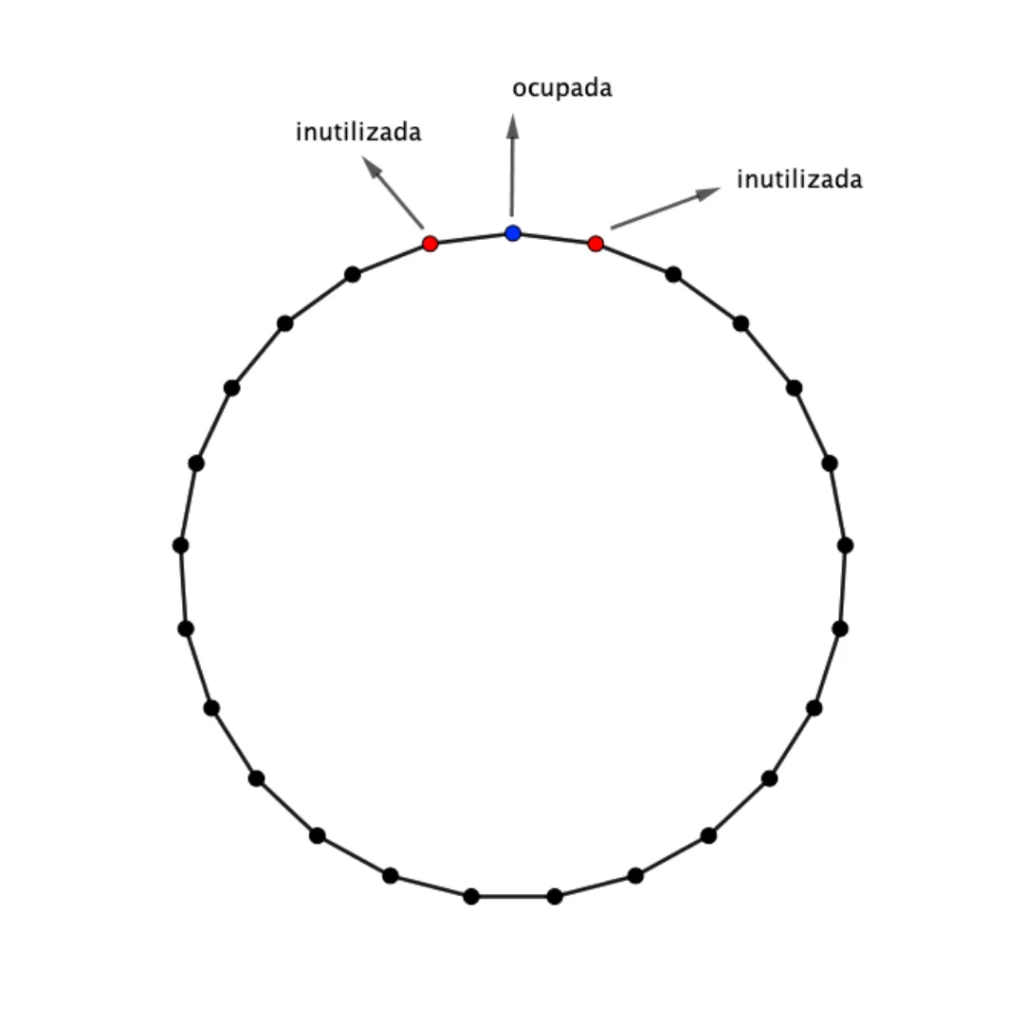
Os vértices da figura representam as cadeiras onde essas pessoas sentarão. Quando uma pessoa senta em uma cadeira, ela “inutiliza” as duas imediatamente adjacentes, conforme ilustrado na figura abaixo:
Como o problema pede o valor mínimo de , o ideal é que não haja cadeiras “inutilizadas” por mais de uma pessoa. Observe a figura abaixo:
Nessa situação final, obrigatoriamente uma pessoa deve sentar à mesa para garantir que a próxima pessoa que venha a sentar, sente-se ao lado de alguém que já esteja sentado.
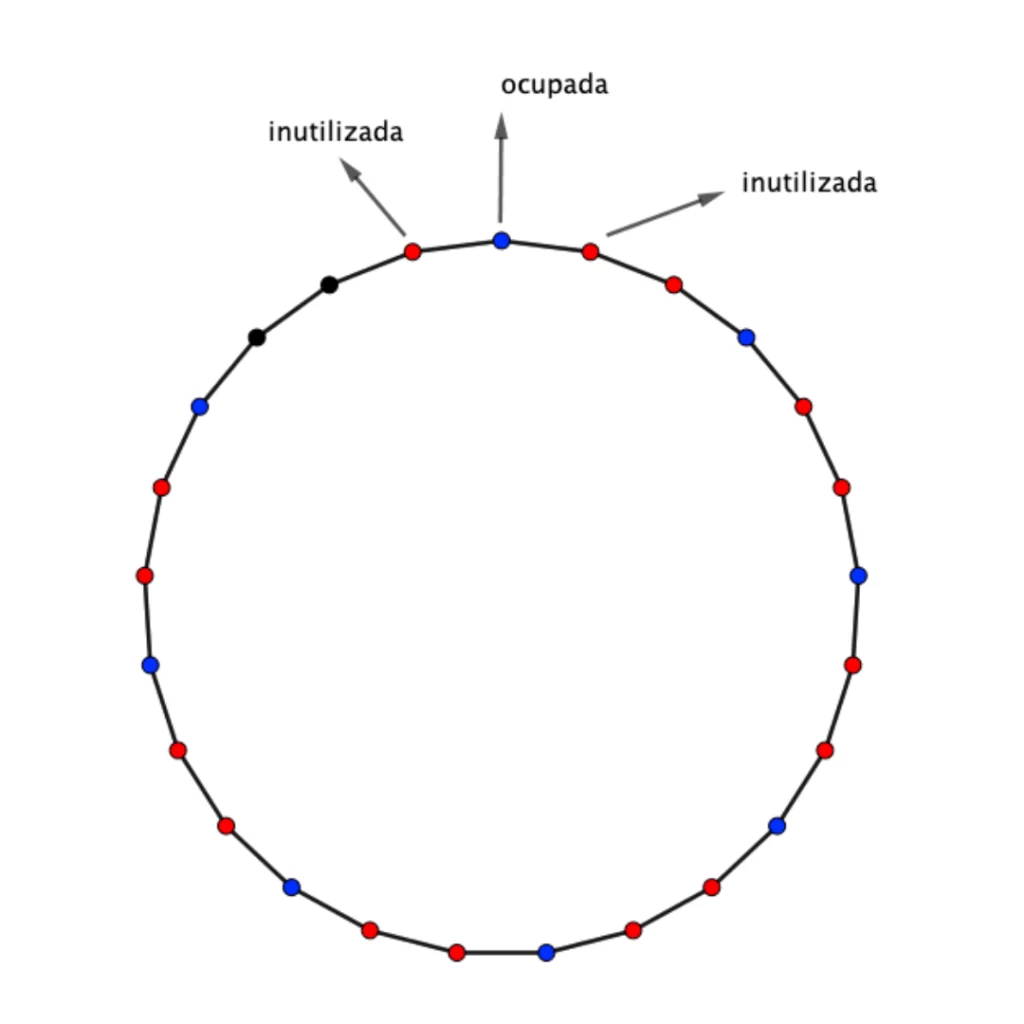
Logo, o número mínimo de pessoas que garante o que o problema pede é igual a 9.
Portanto, o gabarito é a letra B.
