Olá, pessoal! Neste post, vamos resolver juntos a questão 2 da prova de matemática do grupo 2 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Um círculo de centro O é dividido em 12 arcos iguais pelos pontos 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
. Seja Q o ponto médio do arco 
. Considere 
o ângulo entre os segmentos 
e 
.
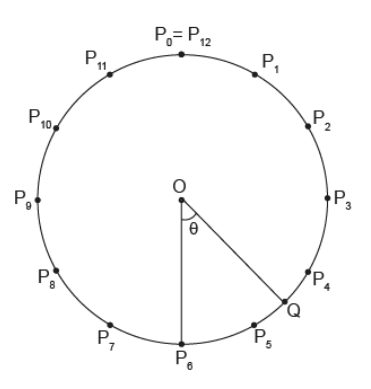
Quanto vale ?
(A) 15
(B) 30
(C) 45
(D) 60
(E) 75
Gabarito: C
Resolução:
A medida de cada um dos 12 arcos iguais obtidos pelos pontos , , , , , , , , , , , , 
é igual a
![\[\frac{360^\circ}{12}=30^\circ\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-b471fc7c270afea9a3dfb95cb90fc526_l3.png "Rendered by QuickLaTeX.com")
Como Q é ponto médio do arco
, temos que: ![\[\begin{array}{rcl}\theta & = & \overset{\frown}{QP_5} + \overset{\frown}{P_5P_6}\\& = & 15^\circ + 30^\circ\\& = & 45^\circ.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-6f08b9daa0ec7b77b8c8bab609bb35e1_l3.png "Rendered by QuickLaTeX.com")
Portanto, o gabarito é a letra C.
