Olá, pessoal! Neste post, vamos resolver juntos a questão 8 da prova de matemática do grupo 2 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
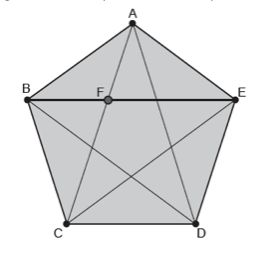
Um segmento de reta está dividido em razão áurea se a razão entre o segmento inteiro e a parte maior for diretamente proporcional à razão entre a parte maior e a parte menor. Assim, por exemplo, sabe-se que uma diagonal de um pentágono regular é dividida em razão áurea pela interseção com outra diagonal. No pentágono regular ABCDE, seja F a interseção entre as diagonais BE e AC, como na figura. Assim, a razão entre BE e FE é igual à razão entre FE e BF. Sabe-se que o comprimento da diagonal BE é igual a 1. Seja 
o comprimento do segmento FE, que é a maior parte da diagonal BE.
Quanto vale ?
(A) 
(B) 
(C) 
(D) 
(E) 
Gabarito: D
Resolução:
Pelos dados do enunciado, podemos afirmar que:
![\[\begin{array}{ll} & \dfrac{BE}{FE} = \dfrac{FE}{BF} \Leftrightarrow\\\vspace{0.2 mm}\\\Leftrightarrow & \dfrac{1}{x} = \dfrac{x}{1-x} \Leftrightarrow\\\vspace{0.2 mm} \\\Leftrightarrow & 1-x=x^2 \Leftrightarrow\\\Leftrightarrow & x^2+x-1=0 \Leftrightarrow\\& \Delta = 1^2-4\cdot1\cdot\left(-1\right)=5\\& x=\dfrac{-1\pm\sqrt{5}}{2\cdot1}\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-cd008e097467093907d3f23c8418ec95_l3.png "Rendered by QuickLaTeX.com")
Como
, concluímos que 
.Portanto, o gabarito é a letra D.
