Olá, pessoal! Neste post, vamos resolver juntos a questão 1 da prova de matemática do grupo 4 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Seja ![]() um triângulo retângulo de lados
um triângulo retângulo de lados ![]() ,
, ![]() e
e ![]() de comprimentos
de comprimentos ![]() ,
, ![]() e
e ![]() .
.
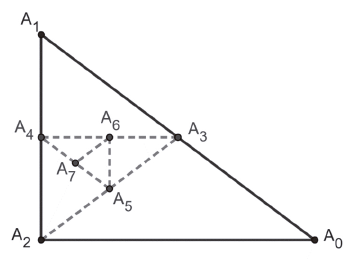
a) Calcule a área do triângulo ![]() .
.
b) Seja ![]() o ponto médio do segmento
o ponto médio do segmento ![]() . Calcule o comprimento do segmento
. Calcule o comprimento do segmento ![]() .
.
c) Seja ![]() o ponto médio do segmento
o ponto médio do segmento ![]() . Mais geralmente, seja
. Mais geralmente, seja ![]() o ponto médio de
o ponto médio de ![]() . Calcule o comprimento de
. Calcule o comprimento de ![]() .
.
Gabarito:
a) 24 u.a.
b) 5
c) ![]()
Resolução
a) Como
![]()
temos que o triângulo
Portanto, a área do triângulo
![]()
b) Como
Por propriedade do triângulo retângulo, temos que a mediana relativa à hipotenusa tem medida igual à metade da medida da hipotenusa.
Portanto,
![]()
c) O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_3A_4 & = & \dfrac{A_0A_2}{2}\\[1em]& = & \dfrac{8}{2}\\[1em]& = & 4.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-1444430897e572610d3b59784bc4a5c5_l3.png)
O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_4A_5 & = & \dfrac{A_1A_3}{2}\\[1em] & = & \dfrac{\frac{A_0A_1}{2}}{2}\\[1em]& = & \dfrac{A_0A_1}{4}\\[1em]& = & \dfrac{10}{4}\\[1em]& =& \dfrac{5}{2}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-4bfd87c8209f4b76a3541cc373c514db_l3.png)
O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_5A_6 & = & \dfrac{A_2A_4}{2}\\[1em] & = & \dfrac{\frac{A_1A_2}{2}}{2}\\[1em]& = & \dfrac{A_1A_2}{4}\\[1em]& = & \dfrac{6}{4}\\[1em]& =& \dfrac{3}{2}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-338b1326370c3fc6f753e4bdd08c5950_l3.png)
O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_6A_7 & = & \dfrac{A_3A_5}{2}\\[1em] & = & \dfrac{\frac{A_2A_3}{2}}{2}\\[1em]& = & \dfrac{A_2A_3}{4}\\[1em]& = & \dfrac{5}{4}\\[1em]& =& \dfrac{3}{2}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-3809335395f4bfa82e4d3c7cf0080dd4_l3.png)
O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_7A_8 & = & \dfrac{A_4A_6}{2}\\[1em]& = & \dfrac{\frac{A_3A_4}{2}}{2}\\[1em]& = & \dfrac{A_3A_4}{4}\\[1em]& = & \dfrac{4}{4}\\[1em]& =& 1.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-bb0fbcace2f160158d65e8e1b6363927_l3.png)
O segmento
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}A_8A_9 & = & \dfrac{A_5A_7}{2}\\[1em]& = & \dfrac{\frac{A_4A_5}{2}}{2}\\[1em]& = & \dfrac{A_4A_5}{4}\\[1em]& = & \dfrac{\frac{5}{2}}{4}\\[1em]& =& \dfrac{5}{8}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-38aba69261a3a87d6824ad37a7f89a48_l3.png)



