Olá, pessoal! Neste post, vamos resolver juntos a questão 3 da prova de matemática do grupo 4 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
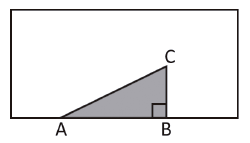
Seja R um retângulo com base igual a 24 e altura igual a 12. Um triângulo retângulo ABC com ângulo reto em B e base AB com comprimento igual ao dobro da altura BC deve ser construído dentro do retângulo R, de forma que a base AB fique sobre a base do retângulo R. Considere 
o comprimento da base AB.
a) Para quais valores de é possível construir esse triângulo?
b) Encontre a expressão da hipotenusa do triângulo retângulo ABC em termos de .
c) Determine o valor de para o qual a área do triângulo ABC é igual a 64.
Gabarito:
a) 
b) 
c) 
Resolução
a) Observe a figura abaixo:
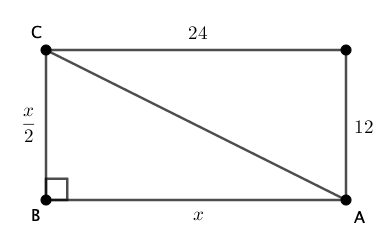
Esse é o maior triângulo que é possível de ser construído dentro do retângulo R.
Portanto, .
b) Pelo Teorema de Pitágoras, temos que:
![\[\begin{array}{rl}& \left(AC\right)^2 = x^2 + \left(\dfrac{x}{2}\right)^2 \Leftrightarrow\\[1em]\Leftrightarrow & \left(AC\right)^2 = x^2 + \dfrac{x^2}{4} \Leftrightarrow\\[1em]\Leftrightarrow & \left(AC\right)^2 = \dfrac{5x^2}{4} \Rightarrow\\[1em]\Rightarrow & AC = \dfrac{x\sqrt{5}}{2}\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-6c5a9f0b629bb458c609109653cab151_l3.png "Rendered by QuickLaTeX.com")
c) Temos que a área do triângulo ABC, em função de
, é igual a: ![\[\dfrac{x\cdot\frac{x}{2}}{2}=\dfrac{x^2}{4}.\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-d7ef1d5a72565b4e76e7e828f90dea3c_l3.png "Rendered by QuickLaTeX.com")
Portanto, para que a área do triângulo ABC seja igual a 64, temos que:
![\[\begin{array}{rl}& \dfrac{x^2}{4}=64 \Leftrightarrow\\[1em]\Leftrightarrow & x^2=256 \Rightarrow\\\Rightarrow & x=16.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-2d6dc9d27f4fe00a4b9ed756e72ccf91_l3.png "Rendered by QuickLaTeX.com")
