Olá, pessoal! Neste post, vamos resolver juntos a questão 1 da prova de matemática do grupo 5 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Seja ![]() a função cujo gráfico está mostrado abaixo. Seja
a função cujo gráfico está mostrado abaixo. Seja ![]() a função definida por
a função definida por ![]() .
.
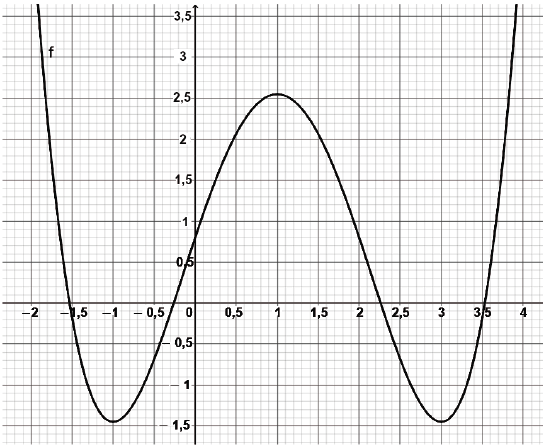
Quantas soluções reais no intervalo fechado ![]() tem a equação
tem a equação ![]() ?
?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Gabarito: C
Resolução
Temos que:
![]()
e
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& g\left(x\right)=0\Leftrightarrow\\[1em]\Leftrightarrow & \dfrac{x}{2}-\dfrac{3}{2}=0 \Leftrightarrow\\[1em]\Leftrightarrow & \dfrac{x}{2}=\dfrac{3}{2} \Leftrightarrow\\[1em]\Leftrightarrow & x=3\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-24a23a8496fb5db4f61cec67ef0acf4d_l3.png)
Como
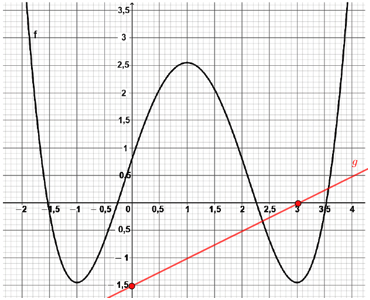
O gráfico da função ![]() intersecta o gráfico da função
intersecta o gráfico da função ![]() em dois pontos.
em dois pontos.
Logo, há 2 soluções reais da equação ![]() no intervalo
no intervalo ![]() .
.
Portanto, o gabarito é a letra C.



