Olá, pessoal! Neste post, vamos resolver juntos a questão 7 da prova de matemática do grupo 5 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Quantas soluções inteiras tem a inequação ![]() ?
?
(A) 0
(B) 2
(C) 4
(D) 6
(E) infinitas
Gabarito: D
Resolução
Vamos iniciar a resolução desse problema buscando, se existirem, as raízes da equação ![]() .
.
Em primeiro lugar, calculemos o discriminante desta equação:
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\Delta & = & \left(-3\right)^2-4\cdot1\cdot\left(-5\right)\\& = & 9+20\\& = & 29\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-2606c514789e8ad3567cc0e84b766719_l3.png)
Substituindo na fórmula resolvente da equação do 2º grau, temos que:
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}x & = & \dfrac{-\left(-3\right)\pm\sqrt{29}}{2\cdot1}\\[1em]& = & \dfrac{3\pm\sqrt{29}}{2}\\[1em]\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-35bde669ef90367291739b8a0fc27925_l3.png)
O gráfico de
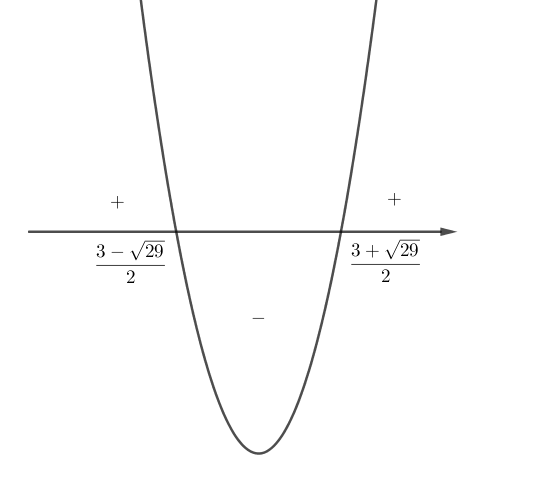
Assim,
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& x^2-3x-5 \leq 0 \Leftrightarrow\\\Leftrightarrow & \dfrac{3-\sqrt{29}}{2} \leq x \leq \dfrac{3+\sqrt{29}}{2}.\\[1em]\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-bc8901d46e2eab929a3c5362f52ef11d_l3.png)
Como
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& \dfrac{3-6}{2}<x<\dfrac{3+6}{2} \Leftrightarrow\\[1em]\Leftrightarrow & -1,5<x<4,5\\\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-4fd33169dc14bc10e1c1ec2cb2f5e613_l3.png)
Então, o conjunto-solução de soluções inteiras da inequação é
Logo, a inequação
Portanto, o gabarito é a letra D.



