Olá, pessoal! Neste post, vamos resolver juntos a questão 3 da prova de matemática dos grupos 1 e 3 do vestibular da PUC-Rio 2024. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Considere a planificação de um prisma ![]() reto cujas dimensões são informadas na figura.
reto cujas dimensões são informadas na figura.
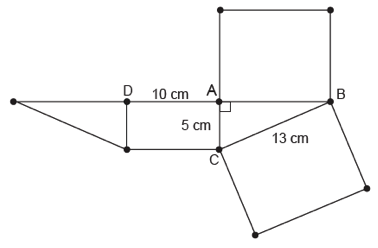
a) Qual é a medida do segmento ![]() ?
?
b) Qual é o volume do prisma ![]() ?
?
c) Considere os pontos ![]() ,
, ![]() ,
, ![]() ,
, ![]() , indicados na figura, como vértices do prisma. Use o plano passando pelos vértices
, indicados na figura, como vértices do prisma. Use o plano passando pelos vértices ![]() ,
, ![]() e
e ![]() para cortar o prisma em dois pedaços. Calcule o volume de cada um dos dois pedaços.
para cortar o prisma em dois pedaços. Calcule o volume de cada um dos dois pedaços.
Gabarito
a) 12 cm
b) 300 cm3
c) 100 cm3 e 200 cm3
Resolução
a) Aplicando o Teorema de Pitágoras no triângulo ![]() , temos que:
, temos que:
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& \left(AB\right)^2+\left(BC\right)^2=\left(AC\right)^2 \Leftrightarrow\\\Leftrightarrow & \left(AB\right)^2+5^2=13^2 \Leftrightarrow\\\Leftrightarrow & \left(AB\right)^2 = 169-25 \Leftrightarrow\\\Leftrightarrow & \left(AB\right)^2 = 144 \Rightarrow\\\Rightarrow & AB=12 \text{ cm.}\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-4852af2cea19ced8526f79575127b010_l3.png)
b) Observe o prisma da planificação dada no problema:
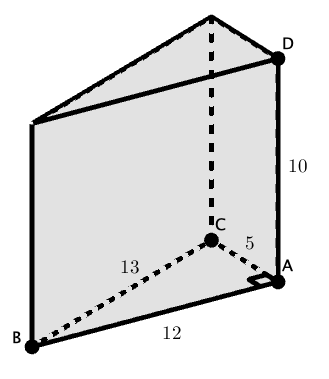
Portanto, o volume do prisma é igual a
![]()
c) Observe a figura abaixo:
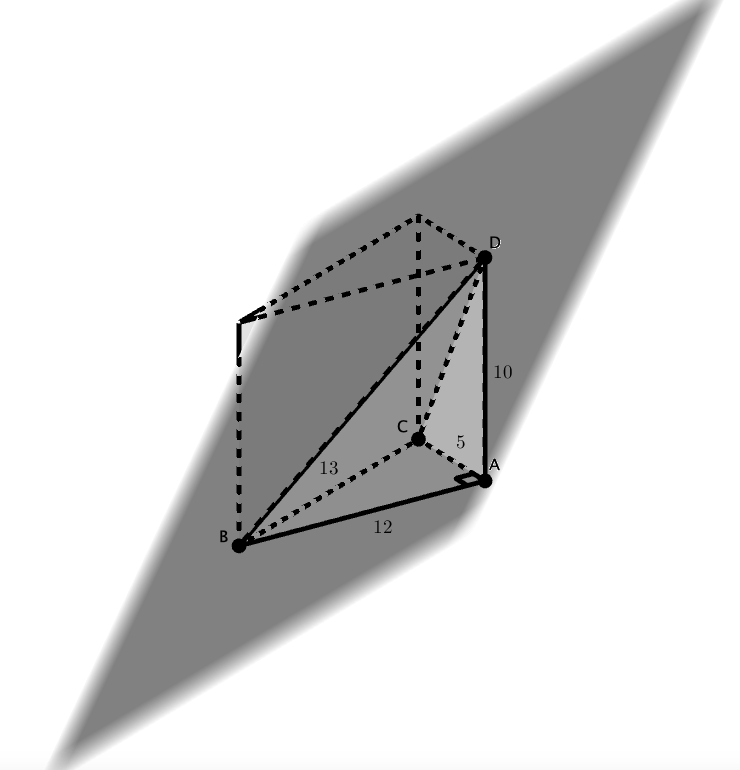
Um dos sólidos obtidos é uma pirâmide de base ![]() e altura
e altura ![]() .
.
Logo, o volume desse sólido obtido pela interseção do plano que passa pelos vértices ![]() ,
, ![]() e
e ![]() com o prisma é
com o prisma é
![]()
Portanto, o volume do outro pedaço do prisma é igual a
![]()



