Olá, pessoal! Neste post, vamos resolver juntos a questão 7 do Exame Discursivo de matemática do vestibular da UERJ 2025. Confira o enunciado e acompanhe a resolução passo a passo, que também está disponível no meu canal do YouTube! Não esqueça de dar um like no vídeo e se inscrever no canal para mais dicas e resoluções como esta. Forte abraço e bons estudos!
Enunciado
Um cilindro circular reto está contido em uma semiesfera de raio ![]() , como ilustra a imagem. O raio
, como ilustra a imagem. O raio ![]() da base desse cilindro mede
da base desse cilindro mede ![]() e o ângulo agudo
e o ângulo agudo ![]() mede
mede ![]() graus.
graus.
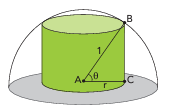
Calcule a altura e a área lateral do cilindro em função de ![]() . Em seguida, calcule o valor de
. Em seguida, calcule o valor de ![]() para que essa área seja máxima.
para que essa área seja máxima.
Resposta
![]() rad
rad
Resolução
Seja ![]() a medida de
a medida de ![]() (altura do cilindro).
(altura do cilindro).
Então, temos que:
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& \sin \theta = \dfrac{h}{1} \Leftrightarrow \\\Leftrightarrow & h = \sin \theta.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-343e6658db9061181b129e92fcc6e748_l3.png)
Além disso,
![]()
Seja
Então, temos que:
![Rendered by QuickLaTeX.com \[\begin{array}{rcl}\left(S_{\ell}\right) & = & 2\pi \cdot r \cdot h \\& = & 2\pi \cdot \cos \theta \cdot \sin \theta\\& = & \pi \cdot 2 \cdot \sin \theta \cdot \cos \theta\\& = & \pi \cdot \sin \left(2\theta\right).\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-d213c9df98f1c0d460187c62137ca537_l3.png)
Como
Portanto,
![Rendered by QuickLaTeX.com \[\begin{array}{rl}& \sin\left(2\theta\right) = 1 \Leftrightarrow \\\Leftrightarrow & 2\theta = \dfrac{\pi}{2} \Leftrightarrow\\\Leftrightarrow & \theta = \dfrac{\pi}{4} \text{ rad}.\end{array}\]](https://www.professorgustavoadolfo.com.br/wp-content/ql-cache/quicklatex.com-6e087cfe037e8479581f5044e651b6f0_l3.png)


